Problem, Apparent Paradox Between Richness and FTLE Variance

1. Problem Statement: Apparent Paradox Between Richness and FTLE Variance

1.1 Observed empirical pattern

First let's look at the data table:

N (Width)	Depth (L)	RA (Rotation)	KA (Kernel)	log10Gλ (Heterogeneity)	Trend
10	2	0.80	0.93	-1.6962 ± 0.0547	Lazy Start
10	6	0.31	0.91	-2.59	Drop
10	8	0.14	0.84	-2.54	Turn
10	12	0.05	0.60	-2.1611 ± 0.2891	Bounce (Increases)
...	...	...	...	...	...
200	2	0.99	0.95	-2.3629 ± 0.1501	Lazy Start
200	6	0.96	0.97	-2.74	Drop
200	8	0.93	0.98	-2.95	Drop
200	12	0.84	0.94	-3.2535 ± 0.1509	Monotonic Drop (Smoother)

From experiments varying width $N$ and depth $L$ :

Wide networks ( $N = 200$ )
As $L$ increases:

RA, KA; ↓ (0.15) while G_{λ}; ↓↓ (0.9)

Representations move away from initialization, yet FTLE variance collapses.

Narrow networks ( $N = 10$ )
As $L$ increases:

RA; ↓↓ (0.75) while G_{λ} \approx const (or rebounds) (0.4)

Strong feature learning occurs without a corresponding increase in FTLE variance.

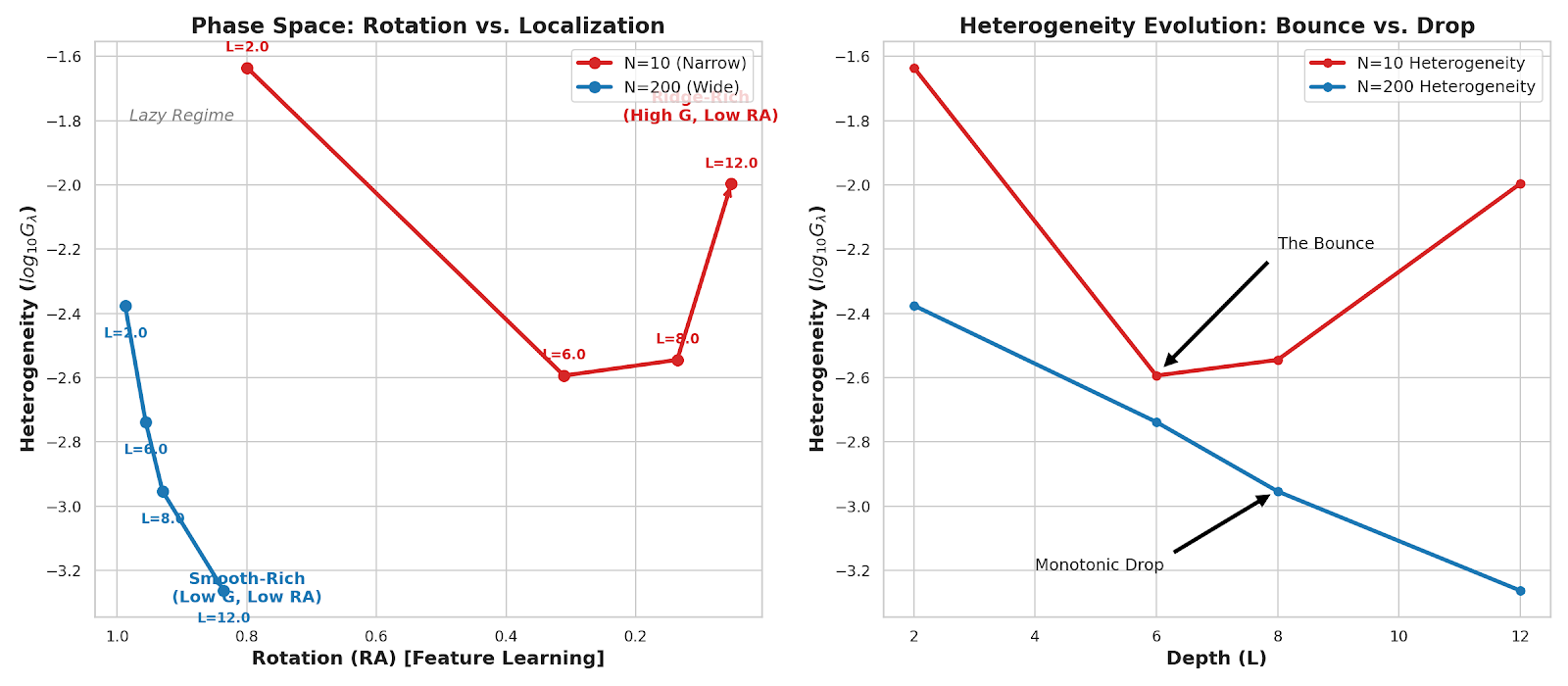
I created a dual visualization to make the "State Space" and the "Bounce" crystal clear.

Left (Phase Space): Notice how N=10 (Red) hooks backward and up into the "Ridge-Rich" zone, while N=200 (Blue) dives down into the "Smooth-Rich" zone.
Right (Evolution): The "Bounce" in $G_{λ}$ for N=10 is clearly visible, contrasting with the monotonic smoothing of N=200.

This appears paradoxical under the naive expectation that “rich learning implies high FTLE heterogeneity.”

1.2 Hidden assumption identified

The paradox relies on an unstated assumption:

rich learning; ⟹; G_{λ} increases .

This assumption is not theoretically justified.

1.3 Metric mismatch diagnosis

The quantities measure different aspects of dynamics:

$RA, KA$ measure global representation motion.
$G_{λ} = {Var}_{x} [λ_{T} (x)]$ measures scalar dispersion, ignoring:
- spatial localization,
- geometric coherence,
- directional alignment of stretching.

Thus, feature motion and FTLE heterogeneity are not required to covary.

1.4 Reformulated problem

The true question is not:

“Why doesn’t $G_{λ}$ increase when learning is rich?”

but rather:

“What kind of FTLE structure corresponds to representation motion?”

This reframing motivates geometry-aware diagnostics beyond scalar variance.

What is missing is a way to distinguish:

rotation vs localization
coherent geometry vs scalar dispersion

This logically motivates the next step: spatial and directional decomposition of FTLE fields.

Theory loading bar (after Step 1)

Identified failure mode of scalar $G_{λ}$
Rejected false equivalence between richness and variance
Motivated spatial + directional decomposition of FTLE

Progress:

[■ ■ ■ □ □]

Next read: First Fix. Radial Decomposition of the FTLE Field